Для изделий, имеющих форму круга, такое решение не подойдет, поскольку у них нет углов, а значит и диагоналей. В этом случае необходим какой-то другой подход, основанный на иных принципах.

И они существуют, причем в многочисленных вариациях. Одни из них достаточно сложные и требуют нескольких инструментов, другие – легкие в реализации и для их осуществления не нужен целый набор приспособлений.
Сейчас мы рассмотрим один из самых простых способов нахождения центра круга с помощью только обычной линейки и карандаша.
Последовательность нахождения центра круга:
1. Для начала нам надо вспомнить, что хордой называют прямую линию, соединяющую две точки окружности, и не проходящую через центр круга. Воспроизвести ее совсем нетрудно: необходимо лишь положить линейку на круг в любом месте так, чтобы она пересекала окружность в двух местах, и провести карандашом прямую линию. Отрезок внутри окружности и будет хордой.
В принципе можно обойтись одной хордой, но мы для повышения точности установления центра круга нарисуем хотя бы пару, а еще лучше – 3, 4 или 5 разных по длине хорд. Это позволит нам нивелировать погрешности наших построений и точнее справиться с поставленной задачей.
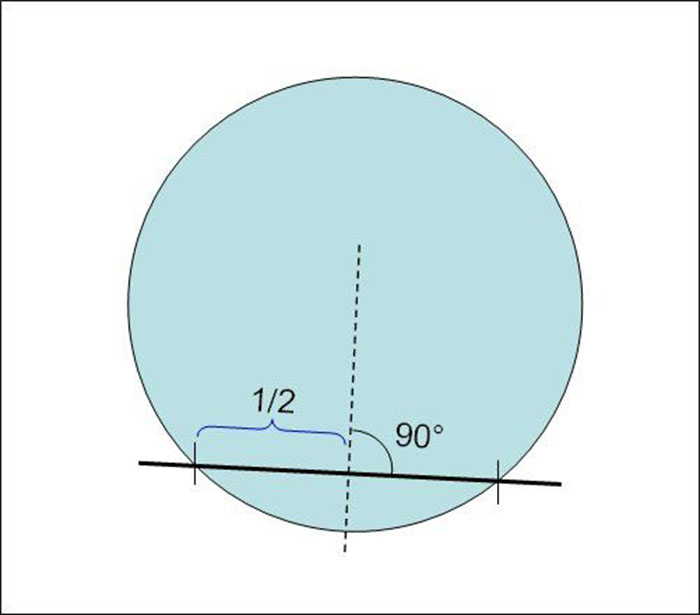
2. Далее, используя ту же линейку, находим середины воспроизведенных нами хорд. Например, если общая длина одной хорды равна 28 см, то ее центр будет находиться в точке, которая отстоит по прямой от места пересечения хорды с окружностью на 14 см.
Определив таким способом центры всех хорд, проводим через них перпендикулярные прямые, используя, например, прямоугольный треугольник.
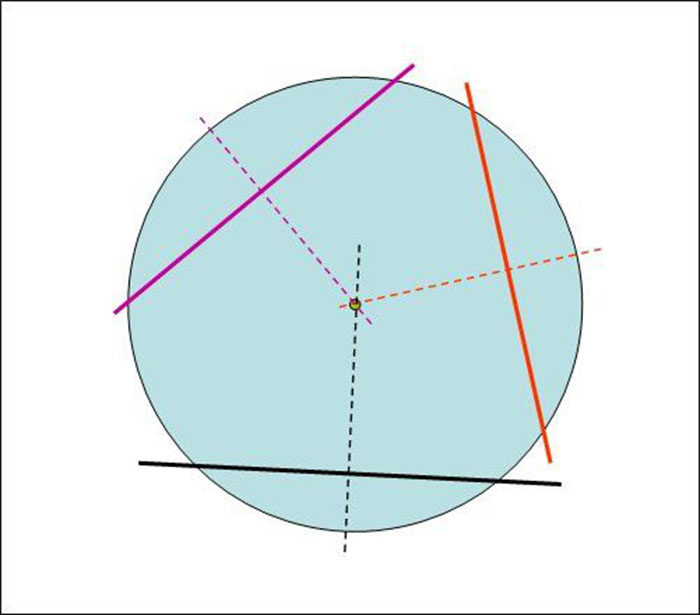

3. Если мы теперь продолжим эти перпендикулярные к хордам прямые в направление к центру окружности, то они пересекутся примерно в одной точке, которая и будет искомым центром круга.

4. Установив местоположение центра нашего конкретного круга, мы можем использовать этот факт в различных целях. Так, если в эту точку поместить ножку столярного циркуля, то можно начертить идеальную окружность, а затем и вырезать круг, используя соответствующий режущий инструмент и определенную нами точку центра круга.
















